‘In India, where only 45% of schools have access to functional computers and just 33% have internet access, unplugged methods to improve Computational Thinking offer a promising solution.’ In this reader submission, researchers Shashaank Varma and Anveshna Srivastava share a simple unplugged sorting activity you can use in your own classroom to develop students’ computational thinking skills.
Imagine a situation where we have to calculate the speed of sound. Now, the first step involves abstracting the nature of the sound wave propagation, which involves conceptualising millions of vibrating particles getting compressed and moving apart rhythmically, to a more tractable model like a single object (a sound ‘wave’) traveling through the air with a constant speed.
Next, we must devise an algorithm to measure the speed of this object. Using the ‘echo’ method, we can record the time it takes to hear an echo from a large wall or building. We can measure the distance from the ‘source’ of the wave object to the wall and then calculate the ratio of the total distance covered to the total time taken.
Next, we can move this ‘source’ further away and try to predict how long the echo would take since now we know its speed. If our prediction is correct, we have found the speed of sound. Otherwise, we can revisit our steps to figure out where we might have erred and then re-calculate the speed.
This process has a sequential nature. It involves abstracting a concept, decomposing the problem into tractable sub-tasks, implementing a step-wise solution, and testing and debugging to arrive at the correct answer. This method of going about things in a precise and structured format so that our solution is systematic and straightforward enough to be converted into instructions for anyone to follow is called Computational Thinking (CT).
Thinking in this manner helps one create solutions that computers can execute, for example algorithmic solutions. The ability to design such solutions is essential to effectively interact with computers and is a major skill that we want to foster in our students.
Educationists have suggested considering CT a fundamental skill along with the reading, writing, and arithmetic skills (Wing, 2006). Such a consideration would involve intervening at a school-going age. Since a majority of the standard interventions for improving CT involve working with computers, they will not work in pedagogical settings where access to computers is limited.
In India, for instance, where only 45% of schools have access to functional computers and just 33% have internet access (UDISE, 2022), unplugged methods to improve CT offer a promising solution. By reaching out to all students, regardless of computer access, these methods have the advantage of being more inclusive.
Here is a simple unplugged task to enhance CT skills that can be easily adapted to various settings.
An unplugged sorting task
Our unplugged method involves a basic sorting task, where we ask middle school students to sort 6 sticks – identical looking and randomly placed – based on their weights. Students are provided with a simple weighing balance to help them comparatively assess the weights (Figure 1).

Figure 1: Students are asked to sort the identical looking 6 sticks based on their weights, by using the weighing balance.
The heaviest stick is only a few grams heavier than the lightest stick and, hence, the task is difficult to perform by proprioception alone.
If we measure the weight of any 2 sticks, we will only know their order in the final arrangement – that is, the heavier one will be placed to the right of the lighter one in an ascending order sorting. But we will not know the exact position of any sticks.
Once the task is done, we carefully weigh one stick after the other to help students verify their solution. We found that students were using 2 distinct methods to do the sorting. Figure 2 illustrates both these methods.
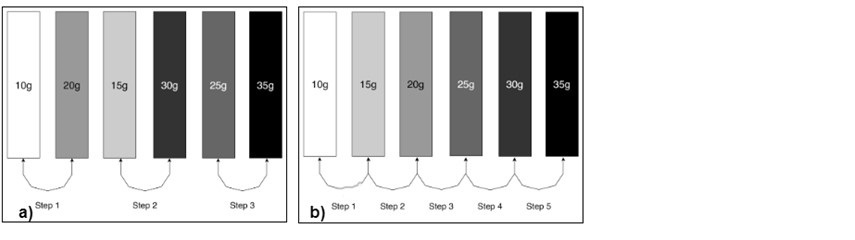
Figure 2: The verification algorithm in 2 forms, (a) the incorrect method, which leads to a positive outcome even when the algorithm is incorrect, and (b) the correct method, both algorithm-wise and outcome-wise.
The first is incorrect because only 2 sticks are compared at a time and the identified heavier stick is not compared with the rest of the sticks. Sometimes it led to the correct response (Figure 2a), but it is not suitable as an ‘algorithm’ or an instruction that could be followed to reach the correct outcome all the time. This contrasts with the second method where a cyclical comparison across the sticks is carried out.
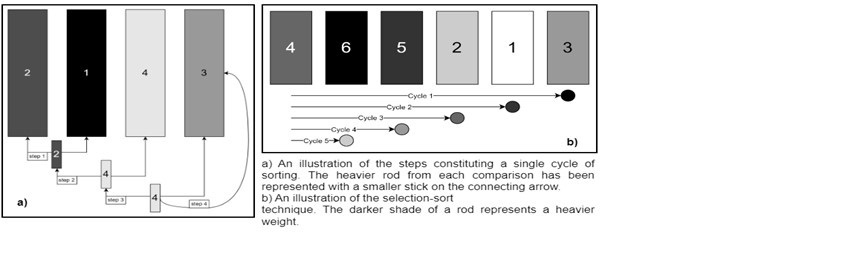
Figure 3: An illustration of the sorting algorithm (selection sort).
This cyclical comparison could be understood in terms of the ‘selection’ sort, where one cycle of comparison is constituted by comparing one stick with all the other sticks (see Figure 3). Next, the remaining sticks undergo the same cycle until they are arranged in ascending order of weight.
If students successfully sorted the sticks, we presented them with the challenge of devising an algorithm that could sort the sticks regardless of their quantity. To aid in this task, we introduced a shorthand notation system that simplified instructions such as ‘Select the stick in slot one and place it on the weighing scale’ to ‘S1 --> W’, where S1 and W represent slot one and the weighing scale, respectively.
This system allowed students to write algorithms quickly and facilitated thinking and translating their thought into the abstract language of ‘codes’. This employs a similar mechanism as in switching to different sets of keywords and syntax while writing a computer program.
What skills can help students succeed?
Twenty middle school students (Mean age = 14.63, SD =2.45, Males=8) participated in the study in their regular classroom.
We correlated their performance on the sorting task with their performance on a standardised CT assessment tool, called CTt (Computational Thinking test), developed by Roman González (2017). Our qualitative assessment tells us that students who were persistent, systematic, and flexible in their methodological approach performed better on the CTt measure.
In a Computational Thinking context, persistent students are adamant about finding a solution. They continue trying even after reaching the limit of attempts. They insist that we give them another shot.
Systematic students approach the problem in a more structured manner – such as by continuing to weigh the sticks in a particular order, from left to right. They may verbalise each step before executing. These practices help the students to mentally cross-check their moves.
Flexible students can easily pick up on different methods and modify these based on evidence.
Takeaways for teachers
Even for students who have access to computers, the sorting and the design of the algorithm tasks provide an excellent method to scaffold the abstraction of concepts – a basic skill for succeeding in computer science. It offers an intuitive platform to constructively engage with the components of CT. Sorting being closely linked to our regular activities provides a fertile context to build the basics of computational thinking.
Teachers can also use other tasks to help their students develop CT skills. An instance is the famous peanut butter and jelly sandwich challenge, where children are encouraged to write an exact recipe for making a peanut butter and jelly sandwich.
It can be extended to other tasks that require sequential, algorithmic execution – such as packing bags for school, or scheduling their morning routine – or complex tasks like searching and navigation.
As in the speed of sound example, students can be presented with problems targeted at various CT skills like decomposition, abstraction, iteration, pattern recognition, and testing in everyday classroom situations.
References
González, M. R. (2015). Computational thinking test: Design guidelines and content validation. In EDULEARN15 Proceedings (pp. 2436-2444). IATED. https://library.iated.org/view/ROMANGONZALEZ2015COM
UDISE, P. (2022). Unified District Information System for Education Plus. Ministry of Education, Department of School Education & Literacy. Government of India.
Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33-35. https://doi.org/10.1145/1118178.1118215
How do you teach Computational Thinking in your own school or classroom? How could you go about incorporating an ‘unplugged’ activity, like the one described in this article? What resources and support would you need?