In the final instalment of his 10-part series on real-world maths, Dave Tout looks at the role of the teacher as a facilitator and resource person.
This final article in the series looks at the critical role of the teacher as a facilitator and resource person and their responsibilities in relation to teaching the mathematics and problem-solving underpinning a context-based teaching approach.
Of course, the ultimate purpose of all this planning is that the students undertake the investigation and learn and apply a range of knowledge and skills.
In order for students to successfully achieve the learning and outcomes expected it is vital that the teacher monitors their progress and intervenes when necessary to teach any identified mathematics and problem-solving skills that are necessary or missing for the task being tackled.
These can be introduced in a number of ways, depending on the skills and experience of the students. This could happen through:
- whole class activities and explanations prior to or during the investigation as questions arise from the students' work;
- small group activities based on explanations, worksheets or tasks provided by the teacher; and,
- individual skills and practice sessions, including worksheets and extracts from textbooks, computers and the internet.
The relationships between the skills, knowledge, practice and context-based problem-solving is illustrated in this diagram:
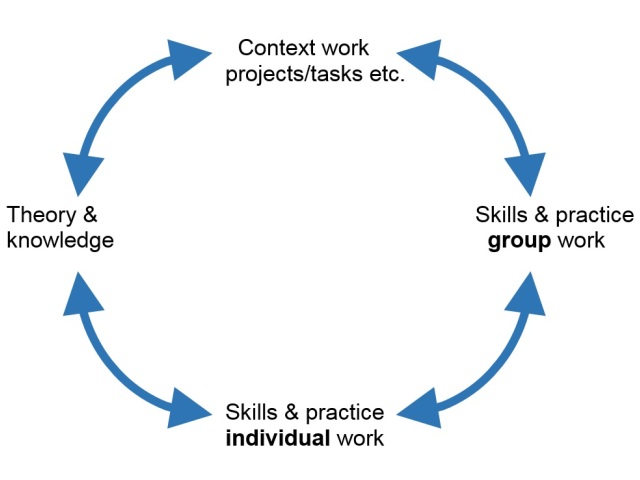
The purpose of using a context-based approach to teaching and learning is that you will start with the context work – the project, task or investigation. So, the cycle might start at the top of the diagram but all the other components are critical and interrelated and are important components of teaching in this way.
The teacher role
In an applied learning or project-based mathematics classroom the teacher plays a critical role. The students need to be supported and guided in order to learn the necessary skills to achieve the desired outcomes. Without this support and direction the investigation and associated learning will not succeed.
The teacher's main role is as a facilitator – there to offer support and advice when needed, and to provide the necessary scaffolding and teaching of skills when necessary. It is vital that teachers remember to teach and instruct their students in any particular skill or piece of mathematical knowledge that is required for the task.
The mathematics skills to develop in students
In this style of teaching and learning, there is a range of different skills that students need to learn. Teachers need to develop students' abilities to:
- identify and recognise how mathematics can be used in real-life situations and contexts, enabling them to make connections between mathematics and the real world (a new skill to many students). This is vital to support students to be able to transfer their skills to new contexts;
- undertake a range of mathematical operations, applications and processes including measuring, counting, estimating, calculating, drawing, modelling and discussing (the underlying mathematical skills and knowledge required to undertake the required investigations or tasks);
- reflect and think about the mathematics they have been using; that is, interpret the results and outcomes of the investigation they have undertaken, including how appropriately and accurately the results fit the situation (another new skill to many students); and,
- represent, communicate and discuss the results and outcomes of the use and application of mathematics in terms of their chosen investigation. This includes both written and oral skills and should incorporate the use of appropriate technologies.
Classroom activities
Depending on the requirements of the task, the teacher will use the motivation of the investigation to have a number of classroom activities ready and available. These will include:
- the work on the investigation/project itself – the initial and ongoing main aim of the activity;
- choosing appropriate intervention times – the teaching and instruction of particular knowledge and skills; what is required to get the job done (for example, if the task requires measurements to be made, then an understanding of measurements and the metric system is fundamental knowledge to be taught); and
- both whole group, small group and individual work on skills and practice on the underlying mathematics skills.
This was illustrated in the above diagram.
Independent vs dependent learners
One important issue that relates to how a teacher might construct the investigation and the classroom activities relates to how independent and capable the students are. Some students may be quite dependent learners with neither independent learning skills nor little learning-to-learn skills. A teacher needs to take this into account and help students move from being dependent to becoming more independent learners.
What this means in the classroom is that lessons and activities need to progress from structured to less structured; from more directed and closed activities to more open ones; from modelled to less modelled; from supported activities to less supported.
The teacher role therefore moves from being a supervisor to being more of a facilitator, scaffolding the learning for the students. Activities and tasks may progress from being provided as small chunks and tasks to being given as larger tasks and projects.
Within the same classroom, some students may undertake the task based simply on the starting open-ended question, whilst others who are less independent or who are lacking specific content knowledge or problem-solving skills may be provided with structured questions, tasks and information that would enable them to still solve the problem. This supports all students, no matter what their level of skill, to be successfully involved in the same investigation and content as other students. The more capable students may go way above and beyond what the teacher wants or expected, but this is one of the positive benefits of teaching this way.
Another way of working with such mixed ability groups in a context-based teaching classroom is to get students to work in small mixed ability groups, where the more capable students help and assist the less capable students. Often this means that all students benefit: the students doing the teaching come to a better understanding of the skills or knowledge being imparted and the learner may understand the content better because it is being explained in the language of their peers.
To read all of the articles in this 10-part series on real-world maths, visit Dave Tout's Teacher author archive.
References
Tout, D., & Motteram, G. (2006). Foundation numeracy in context. Australian Council for Educational Research (ACER). Camberwell: Victoria.
What roles do you play and what strategies and processes do you use to support your learners when undertaking an investigation in (or outside) your classroom?
How do you scaffold learning for your students? Think about a topic you’re teaching next term that involves an investigation – how can you break it down into smaller chunks and tasks?
Do you use classroom activities that reflect the real-life situations that your students are likely to face beyond the school gates?



