Progress in life is often made in small, incremental steps. But occasionally, advances are made in leaps—for example, when the penny drops and something is seen in an entirely new light.
In his book The Structure of Scientific Revolutions, Thomas Kuhn observes that progress in science occurs not only in small increments, but through occasional fundamental shifts in how scientists see and understand some aspect of the world. (Kuhn, 1962)
Kuhn refers to such shifts in perspective as changes in the ‘paradigm’ within which scientists work. At any given time, the prevailing paradigm consists of current theories, concepts, supporting technologies, methods and literature, which together enable what Kuhn refers to as the practice of ‘normal’ science.
But occasionally normal science encounters unexpected observations that are inconsistent with existing paradigm. When this occurs, the initial response is not to reject the current paradigm, but to attempt to modify it to accommodate the problem. If this cannot be done, the existing paradigm comes under increasing pressure and, within the relevant scientific community, there may be a growing sense of crisis.
It is under these conditions that an alternative paradigm may emerge, offering to better address the problem that has led the old paradigm into crisis. This proposed paradigm offers a different way of thinking and, ultimately, a new approach to ‘normal’ science.
Kuhn observes that the introduction of a new paradigm is always controversial. There is inevitably opposition to paradigm change, especially from those who have spent their scientific careers working within the earlier paradigm. Change, if it occurs, usually takes considerable time and occurs through a growing shift in the distribution of professional allegiances.
The relevance of this to school education is that schools also can be thought of as operating within a prevailing paradigm. This paradigm has theoretical underpinnings, concepts, rules and methods that guide ‘normal’ practice. However, as occasionally occurs in a field of practice, a significant mismatch currently exists between theory and observation; normal practice in school education is not delivering the results it was expected to deliver.
The prevailing paradigm
Most schools operate under a shared set of intentions, practices and ways of thinking about teaching and learning. In this sense, they operate within a common paradigm.
One element of these shared intentions, practices and ways of thinking is the school curriculum. Under the prevailing paradigm, the role of the curriculum is to spell out what teachers should teach and students should learn in each year of school.
If there is a ‘theory’ underlying this paradigm, it is that all students in a year level are able to engage meaningfully with, and benefit from, the year-level curriculum, and are capable of mastering the content of this curriculum if they make the necessary effort.
It is recognised that some students may require additional support to be able to do this, and teachers are encouraged to ‘differentiate’ their teaching to provide additional assistance to students who require it. But the assumption underlying normal school practice is that all students are capable of success on year-level curricula with the requisite effort and appropriate support.
The anomaly
The anomaly in current practice is that observations of student learning and performance are not consistent with the assumptions and expectations of the paradigm under which schools operate.
The problem is readily apparent in well-constructed measures of student attainment such as those displayed in Figure 1 (Siemon et al, 2019). The distributions in Figure 1 were produced by a team of mathematics education researchers.
The researchers began by constructing a scale for measuring levels of mathematical proficiency. This numerical scale was then divided into eight levels that represent absolute levels of mathematics knowledge and skill, independent of age or year level.
They then tested samples of Australian students in each of Years 5, 6, 7, 8 and 9 and used students’ test performances to allocate them to one of the eight proficiency levels. The distributions in Figure 1 are the result of those allocations.
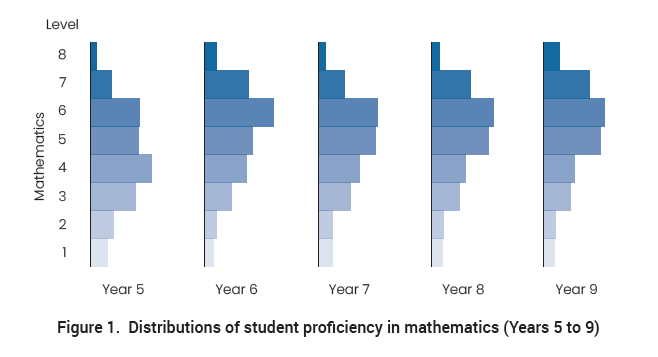
Figure 1. Distributions of student proficiency in mathematics (Years 5 to 9)
From Figure 1 it can be seen that, in each year group, some students performed at each of the eight proficiency levels. There was a small percentage of students in Year 5 already performing at level 8, and a small percentage of students in Year 9 still performing at level 1, and everything in between.
Conclusions of this kind are reached routinely in analyses of student performance in all areas of learning for which reliable measures are available. In each year of school in Australia, the most advanced 10 per cent of students in any year group are between five and six years ahead of the least advanced 10 per cent of students. There is thus a significant mismatch between the empirical evidence and the assumption underlying normal practice—that students in the same year group are more or less equally ready for, and able to benefit from, the same year-level curriculum.
This mismatch is commonly attributed to factors other than the paradigm itself—for example, to underperforming teachers, underfunded schools, changes in society or a lack of student effort. While these may all be contributors, the schooling paradigm itself is the root cause.
An alternative paradigm
The basis for an alternative paradigm is contained in Figure 1. Under this alternative, rather than developing a curriculum for all students in each year of school, a mathematics curriculum is developed for each of the eight proficiency levels in Figure 1. This requires a switch in focus—from the horizontal axis (time) to the vertical (proficiency). Instead of inferring what a student is ready to learn next in mathematics from their year level, this is inferred from their demonstrated level of mathematics proficiency, whatever their age.
In essence, this alternative paradigm makes mastery rather than time the basis of advancement through the curriculum. Rather than being required to move to the next year’s curriculum because time has elapsed, students do not progress to the next proficiency level until they have mastered the prior level. The consequence is that students may progress at different rates. Those who require more time have it; those ready to move to the next level are able to do so.
Figure 1 suggests that a mathematics curriculum developed for any one of these eight proficiency levels is likely to be appropriate for some students in each of Years 5 to 9. Curricula developed at these eight levels are likely to be appropriate for most students across at least seven years of school, meaning that the number of mathematics curricula to be developed under this alternative would be similar to the current number of year-level curricula. This immediately raises the question of how a teacher could manage a classroom in which students were working at eight different levels.
In practice, most teachers could probably manage students working at two or three different levels, but it is difficult to imagine most teachers managing more than this. Schools in which students vary widely in their levels of attainment may need to find ways of having teachers collaborate to ensure every student is taught at a level appropriate to their current learning needs.
Making the change
In science, Kuhn argued resistance to an alternative paradigm is both ‘inevitable and legitimate’. Change does not occur easily and, when it does occur, is not justified by ‘proof’ but by the perceived possibility of a better way of addressing an existing problem (Kuhn, 1962). Perhaps similarly, a changed way of thinking about teaching and learning in schools should not occur easily.
According to Kuhn, a crucial step in making the change to a different way of thinking and working in science is the development of a ‘clear exhibit’ of what scientific practice would be like under the alternative. Any change to the structure of school learning is likely to depend on a clear illustration of what change would look like in practice, including the implications for future teaching and learning.
For this reason, change should be introduced cautiously. Ideally, work would begin in just one or two areas of learning, with curricula in these areas being redeveloped as proofs of concept. Essential to restructuring any curriculum will be a dependable body of empirical research into how knowledge, skills and understandings in that subject unfold and are best developed over time. An obvious starting point would be mathematics, given considerable research into the progression of learning in that subject.
At the heart of a restructured curriculum will be a relatively small number of essential concepts, principles and methods to be developed in increasing depth over a number of years of school. Important factual and procedural knowledge usually will be organised around these core understandings. Concrete examples of development—in the form of samples of student responses and work—will be essential to illustrate the levels of the restructured curriculum. And, ideally, these descriptions and illustrations will be accompanied by extensive advice, resources and associated professional learning for teachers.
This alternative paradigm is more than a different way of structuring the curriculum; it invites new ways of thinking about teaching, learning, assessment and reporting—in a sense, a redefinition of ‘normal’ practice.
This is an edited version of the essay, Time for a paradigm shift in school education?, by Professor Geoff Masters AO. Read the full version on the ACER website.
References:
Kuhn, TS. 1962. The structure of scientific revolutions, University of Chicago Press.
Siemon, D., Barkatsas, A., & Seah, R (eds). (2019). Researching and using progressions (trajectories) in mathematics education. Brill. https://brill.com/view/title/54651
