Differentiating instruction to better meet the needs of all learners is not new. It recognises that in any classroom there are significant differences between students in terms of their prior knowledge, experience, preferred ways of learning and their social and emotional predispositions to learn.
'Educational researchers have known for decades that a student learns best when teaching is targeted to what she is ready to learn. If the material is too easy, students can become bored and disengage. If it is too hard, students will flounder and may choose to misbehave or give up rather than face continued failure. In either case, little is learnt. But if teaching is targeted at what students are ready to learn, powerful progress can be made.” (Goss, Hunter, Romanes & Parsonage, 2015)
Requirements of targeted teaching
From my perspective, targeted teaching is a form of differentiation that is specifically concerned with student's learning needs in relation to several ‘big ideas' in number, without which their progress in school mathematics will be seriously impacted. It requires:
- assessment tools and techniques that expose students' thinking and provide valid and reliable information about where students are ‘at' in relation to an important big idea;
- a grounded knowledge of underlying learning progressions, key steps in the development and application of big ideas and how to scaffold these;
- an interpretation of what different student responses might mean and some practical ideas to address and progress student learning (i.e., where to go to next);
- an expanded repertoire of teaching approaches that accommodates and nurtures discourse, helps uncover and explore student ideas, and ensures all students can participate in and contribute to the enterprise;
- time with students to develop trust and supportive relationships; and
- the flexibility to spend time with the students who need it the most (Siemon, Virgona & Corneille, 2001).
This notion of targeted teaching was prompted by the findings of two large-scale projects that revealed a seven to eight year range in mathematics achievement in each year level in the middle years of schooling (Siemon, Virgona & Corneille, 2001) that was explained by student's access to multiplicative thinking (Siemon, Breed, Dole, Izard & Virgona, 2006).
Multiplicative thinking is the conceptual and strategic knowledge needed to work efficiently and confidently with larger whole numbers, fractions, decimals and percent and to solve an extended range of problems involving multiplication and division including proportional reasoning. Access to this kind of thinking is needed to successfully engage with school mathematics beyond Year 5 and realistically aspire to further STEM-related studies.
Data from the Scaffolding Numeracy in the Middle Years (SNMY) project, the second of the two studies mentioned above, found that approximately 70 per cent of Year 5 and 35 per cent of Year 8 students did not have access to multiplicative thinking. A 2014 study that used the same tools to assess multiplicative thinking in over 1700 Year 7-9 students from lower socio-economic schools found that the proportion for Year 8 students was closer to 55 per cent (Siemon, Milne, Sharpley & Vanderpal, 2014).
Targeted teaching to big ideas works
Analysis of the SNMY data led to the identification of an eight-level Learning and Assessment Framework for Multiplicative Thinking (LAF). Teaching advice was prepared for each level (referred to as ‘zones') to help teachers consolidate the knowledge and skills identified at that zone and scaffold what was needed for students to progress to the next zone in the framework.
Teaching targeted to students' identified learning needs in relation to the LAF resulted in effect sizes of 0.45 to 0.75 or more in research schools, compared to effect sizes of 0.2 to 0.5 in reference schools. Breed's (2011) 18 week intervention, conducted as part of the SNMY project, involved nine Year 6 students identified in Zone 1 of the LAF. When re-assessed three months after the intervention, all nine students shifted at least four zones, with the majority shifting five zones to be age and grade appropriate.
In 2013, SNMY data was obtained from 28 schools located in lower-socio economic settings in the Northern Territory, Queensland, South Australia, Tasmania and Victoria. Matched data sets were obtained from 1732 students from Years 7-10 with the majority (59 per cent) from Year 8. Although the results varied considerably between schools, the overall achievement of students across the 28 schools represents an average effect size of 0.6, which can be seen the shift in the relative proportions in each zone of the LAF from August to November shown in Figure 1.
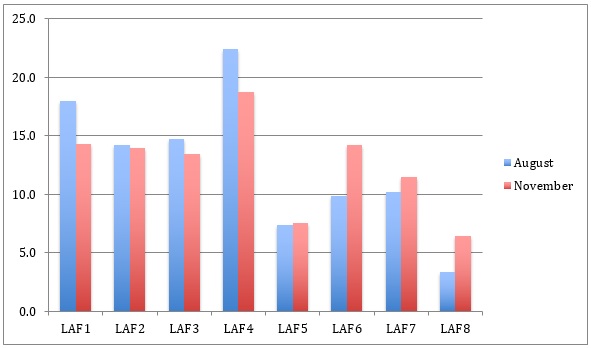
[Figure 1: Proportion of students by LAF zone in August and November 2013.]
Targeted teaching F-10
While the SNMY assessment options and teaching advice can be used with students from Years 4-9, something more is needed to help prevent, or at least substantially reduce, the seven to eight year range in mathematics achievement in the middle years. As a result of unpacking the zones, I identified six ‘big ideas' in number that need to be in place by the end of key levels of schooling to ensure students are ready to learn what is needed to progress confidently in school mathematics. Not surprisingly, most relate in some way to the development of multiplicative thinking.
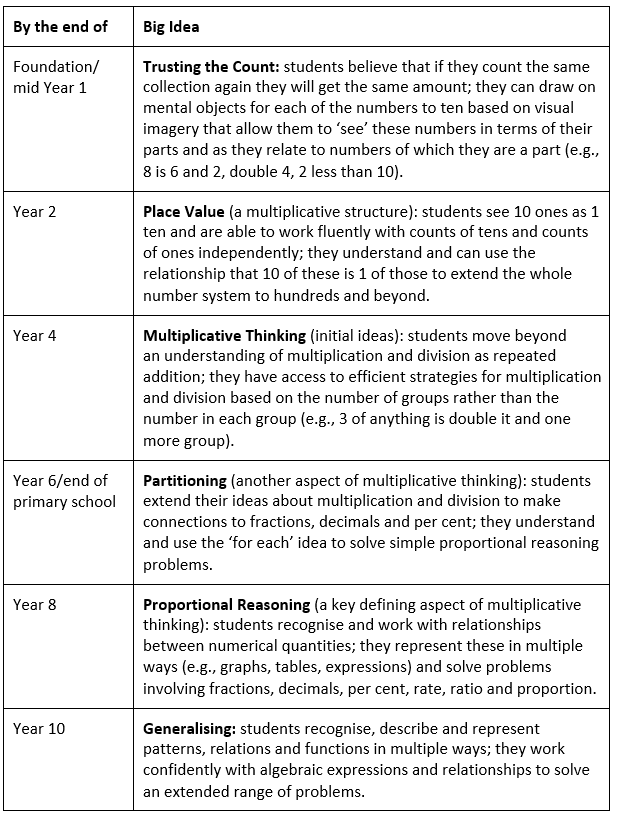
[Table 1: The big ideas in Number by key levels of schooling (Siemon, 2006).]
A suite of performance-based, one-on-one interview tasks were developed to evaluate key aspects of each of these big ideas. These are supported by a range of student responses to each task, an interpretation of what each response means and specific teaching advice to assist teachers recognise and build on what the student already knows and can do. Known as the Assessment for Common Misunderstandings, these resources are bow being used to support targeted teaching and improve mathematics learning outcomes in primary schools in the Australian Capital Territory, Queensland, South Australia, Tasmania and Victoria.
Some final thoughts
In conclusion, targeted teaching is characterised by an unrelenting focus on ‘big ideas', without which students' progress in mathematics will be seriously impacted.
It takes time and effort. Our experience to date has shown this to be a very organic process that schools appropriate and implement according to their circumstances. Targeted teaching is most effective where it has evolved over time with the support of key individuals and the leadership group and the provision of targeted professional learning.
References
Breed, M. (2011). Constructing paths to multiplicative thinking. Unpublished PhD Thesis, RMIT University.
Goss, P., Hunter, J., Romanes, D., Parsonage, H. (2015). Targeted teaching: how better use of data can improve student learning, Melbourne: Grattan Institute.
Hattie, J., (2012). Visible Learning for Teachers, Maximising Impact on Learning. Routledge, Oxford: UK.
Siemon, D. (2006). Assessment for Common Misunderstandings Materials. Prepared for and published electronically by the Victorian Department of Education and Early Childhood Development. http://www.education.vic.gov.au/school/teachers/teachingresources/discipline/maths/assessment/Pages/misunderstandings.aspx
Siemon, D., Breed, M., Dole, S., Izard, J., & Virgona J. (2006). Scaffolding Numeracy in the Middle Years – Project findings, materials and resources, Final report submitted to Victorian DET and Tasmanian Department of Education http://www.education.vic.gov.au/school/teachers/teachingresources/discipline/maths/assessment/Pages/scaffoldnum.aspx
Siemon, D, Milne, G., Sharply, B. & Vanderpal, S. (2014). The Final Report of the Australian Mathematics and Science Partnership Priority Project: Reframing Mathematical Futures. Unpublished report submitted to the Australian DET. RMIT University: Melbourne
Siemon, D., Virgona, J. & Corneille, K. (2001). The Final Report of the Middle Years Numeracy Research Project: Retrieved from http://www.education.vic.gov.au/school/teachers/teachingresources/discipline/maths/Pages/mynr.aspx
How are you monitoring individual student progress?
How do you know when students are confident in their learning and ready to move on to the next steps?
As a school leader, what whole school intervention strategies are you implementing to identify and support students who are falling behind in mathematics?



