So far in a 3-part series on teacher planning, educational leader Michael Rosenbrock has looked at how teachers can pro-actively plan to tackle student misconceptions in STEM, and planning to support students to build and use their vocabulary in science and mathematics. In this final article, he explores how teachers can best plan to make effective use of manipulatives and representations to help students build understanding.
There are many concepts in mathematics and science – such as the multiplication of fractions or the behaviour of subatomic particles in the atom – that require either abstract understanding, or relate to a scale or context that is beyond our experience of reality.
To address this, teachers frequently use manipulatives and representations to support students to build understanding. Planning to do so effectively can have a positive impact on student learning.
Planning to make effective use of manipulatives and representations is aligned with the Australian Professional Standards for Teachers 1.2 Understand how students learn, 2.1 Content and teaching strategies of the teaching area, 2.2 Content selection and organisation and 3.2 Plan, structure and sequence learning programs.
What exactly are the manipulatives and representations this article focuses on? Broadly, they are tools that can support and scaffold the building of understanding of concepts. Specifically:
- Manipulatives are objects that can be interacted with to support learning. Examples include blocks, rods, buttons, and physical or virtual models.
- Representations are forms in which knowledge can be presented, explained, or explored. Examples include fractions on a number line, algebraic expressions, symbols, diagrams, graphs, and conceptual models.
Daniel Willingham (2017) suggests that effective use of manipulatives may be understood by thinking of them as providing analogies that support extending existing knowledge to something new. It can be helpful to keep this framing in mind, as many uses of manipulatives and representations have some element of analogy or metaphor underpinning them.
The evidence on manipulatives and representations
Evidence for Learning’s (E4L) Guidance Reports on science, mathematics, and metacognition draw on extensive reviews of the available evidence to make practical, evidence-informed recommendations (Evidence for Learning, 2019, 2020, 2022, 2023). They include several key considerations relating to manipulatives and representations:
- Keep in mind that they are just tools, use them purposefully and appropriately for impact.
- They can support students to access concepts that are abstract or outside our everyday experience, building a bridge between current ideas and new thinking.
- Be clear on the rationale for their use to build understanding of a specific concept.
- They can be used effectively at different ages and stages.
- Enable students to understand the connections between them and the concept.
- Avoid students focusing on irrelevant or superficial features that do not build understanding.
- Be aware of their limitations, support students to compare them and appreciate their limits, where relevant.
- Use as a scaffold and avoid students becoming over reliant on them, encourage use of more abstract representations as appropriate.
- Ensure that any explicit analogies or metaphors used are familiar to students, so that they are supportive rather than a hindrance.
- Keep in mind cognitive load – avoid introducing too much detail or too many manipulatives and representations at one time.
- Plan for consistency in their use across levels and subjects to avoid confusion or developing misconceptions.
- Support students to use manipulatives and representations judiciously when solving problems, communicating their thinking, or planning-monitoring-evaluating their learning.
Using manipulatives and representations in practice
What would it look like if we put this evidence into practice in maths and science teaching? Let’s look at a few examples from across the F-12 curriculum.
Using number lines in mathematics
Number lines can be a particularly effective teaching tool in mathematics (Evidence for Learning, 2020). In the Australian Curriculum at year 6 level, students encounter addition and subtraction of fractions using knowledge of equivalent fractions (ACARA, 2022a). A common error at this stage is adding both the numerators and denominators. A teacher could plan to address this explicitly with students through a prompt as follows (Evidence for Learning, 2020).

At this level students are likely to have existing knowledge of and experience working with a number line. They could then be supported to check their understanding by representing the two fractions on a number line as shown below (Evidence for Learning, 2020). This representation clearly shows that 2/10 cannot be the correct answer. Students can then be supported to recognise that 1/2 is equivalent to 4/8 and use this knowledge to correct the equality statement above.

Supporting students to understand number lines and use them effectively can also provide them with a tool they can draw upon when they get stuck. One way a teacher could build this capacity is to prompt a student to ‘try representing the values on a number line’.
Number lines are not limited in their use to primary school settings. They can be used in representing simple inequalities such as x > 3, are a helpful building block to understanding the cartesian plane, and may assist with introduction of the complex plane in senior secondary.
Electric circuit models in science
Building student understanding of electric circuits can be challenging as it relates to phenomena we cannot observe and concepts such as electric fields that are not accessible until senior secondary and beyond.
Using simple models can be helpful for developing key concepts such as current and voltage. However, it is important to be conscious of not developing misconceptions. Three models that are commonly used are the water circuit, rope model, and delivery van or jellybean model (Evidence for Learning, 2022).
Figure 1. Adapted from E4L’s Models for electric circuits (Evidence for Learning, 2022). Click here for an enlarged version of the image below.
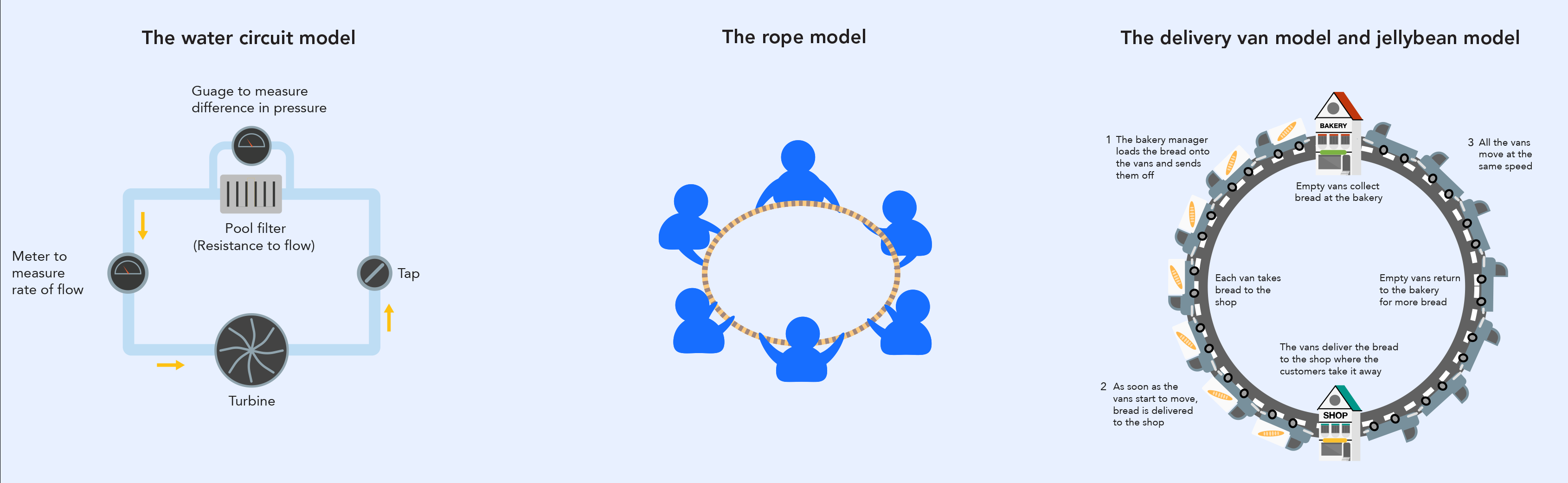
Each of these models has limitations in what they can and cannot represent. Teachers using these models will require a strong understanding of their limitations and the underlying concepts to make the most effective use of them. The rope and jellybean model can both be used as a role play during a lesson. It is important to ensure students don’t get distracted by the irrelevant features, particularly with the jellybean model!
Comparing models can help students to understand the underlying concepts, for example by exploring what concepts they can represent, what is missing, and what is different (Evidence for Learning, 2022). Using a knowledge organiser can support students to organise their critique of the models.
Virtual models can also be used, such as the Circuit Construction Kit from the University of Colorado’s PhET project. Such models can be advantageous in that they can ‘show’ representations of the ‘inner workings’ of a model, such as the flow of current that we cannot see in an experiment with a physical circuit. This can further assist with understanding common points of confusion, such as the difference between the direction of conventional current and electron movement. The ability to understand and effectively use virtual models can also support students to check their own understanding against the model or try a different approach if they are stuck.
Physical manipulatives in mathematics
It is common to use physical manipulatives in mathematics and they can be used effectively across primary and secondary levels in the appropriate context (Evidence for Learning, 2020).
In the later years of secondary mathematics students will encounter the use of Pythagoras’ theorem in a 3-dimensional shape. Students can find it challenging to accurately visualise such scenarios and apply the theorem appropriately.
A simple physical manipulative of a 3D rectangular prism made of straws or another readily available material can support students to build their understanding. Using different colours for each of the sides and a string for the diagonals can help avoid confusion. Students could be tasked with measuring and recording the side and diagonal lengths and representing the scenario with drawings in their workbook. They could then use Pythagoras’ theorem to calculate the diagonal and compare to their measurements.
The scaffolding provided by such a manipulative can likely be removed with relative ease. However, having an exemplar object available in class may allow students to access the representation again later if they get stuck.
Questions for teachers to consider
- Where do you currently use manipulatives and representations to build student understanding?
- How can you ensure students make connections between them and the concept?
- Are the metaphors or analogies that underpin the manipulatives and representations that you use sufficiently familiar to students?
- Where within your planning might it be beneficial to build in opportunities for students to compare them or consider their limits?
- What approaches could you use to ensure they are an effective scaffold?
- How might you collaborate with colleagues to ensure consistency in the use of manipulatives and representations across levels and subjects?
- Are there opportunities for building student capacity to draw on manipulatives and representations when they get stuck in their learning?
Key takeaways
- Manipulatives and representations are tools that can be used effectively to support students to build understanding across ages and stages.
- It is important to be aware of their limitations and avoid overloading students with too much new information at once.
- Deliberately planning when and how to use them can help to ensure that they are an effective scaffold and avoid confusion or developing misconceptions.
References
ACARA. (2022). AC9M6N05, Mathematics: Number: Year 6. Australian Curriculum v9.0. Author. https://v9.australiancurriculum.edu.au/f-10-curriculum.html/learning-areas/mathematics/year-6/content-description?subject-identifier=MATMATY6&content-description-code=AC9M6N05
Evidence for Learning. (2019) Metacognition and self‐regulated learning. Evidence for Learning. Available from http://e4l.org.au/metacognition
Evidence for Learning. (2020) Improving mathematics in upper primary and lower secondary. Evidence for Learning. Available from http://e4l.org.au/maths-primary-secondary
Evidence for Learning. (2022) Improving secondary science. Evidence for Learning. Available from http://e4l.org.au/science-secondary
Evidence for Learning. (2023). Improving mathematics in the early years with children aged
3‐7 years. Evidence for Learning. Available from https://e4l.org.au/early-maths
Willingham, D. (2017) Ask the Cognitive Scientist: Do Manipulatives Help Students Learn?
American Educator, Fall 2017. https://www.aft.org/ae/fall2017/willingham
Evidence for Learning is developing a resource focused on putting evidence to work in STEM, which you can find here: https://e4l.org.au/stem-in-schools



