In Leading Improvement in Mathematics Teaching and Learning, Monash University Emeritus Professor Peter Sullivan ‘provides a framework for a set of high-impact strategies that individually and together can be the focus of teacher professional learning, school improvement and student numeracy achievement.’
In supporting school leaders, the book unpacks how high-impact strategies and practices can be applied to achieve improvement goals. This exclusive extract for Teacher readers is taken from the chapter Practice 1: Quality classroom learning experiences as a focus of teacher professional learning.
Choosing classroom tasks
To show how discussions might proceed, the following is an example of a classroom task suitable for Foundation level, but also relevant at most levels of primary school. There is also a task suitable for middle years students. The first task is from the ‘Exploring mathematics sequences of connected cumulative challenging tasks project, conducted by Monash University (Sullivan et al. 2019).
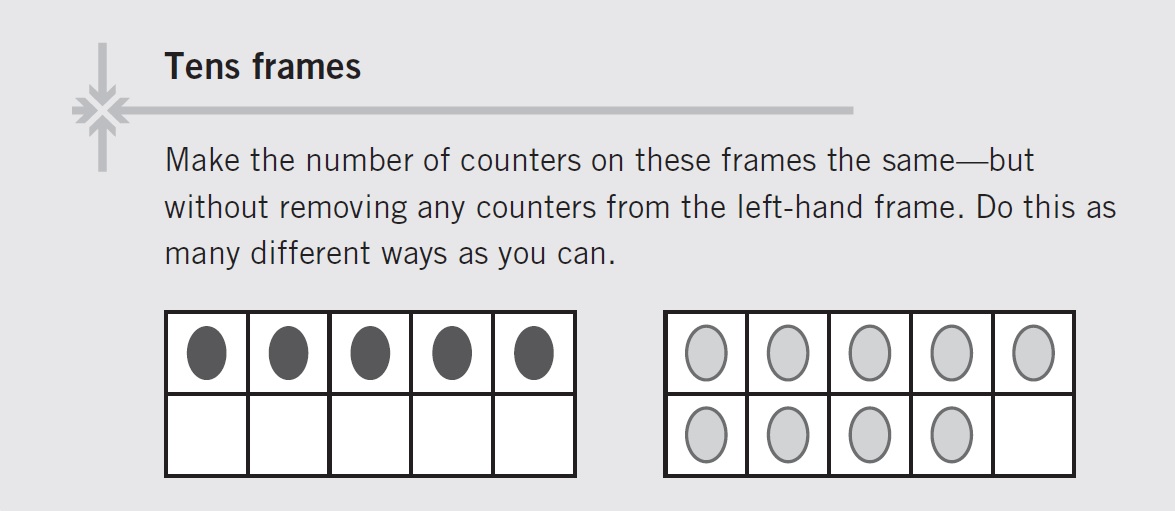
Readers are invited to find five distinct solutions. There are some obvious solutions, but there are also others that require some lateral thinking. The task can be readily modelled. The focus of this task is on more, less, equivalence, addition and subtraction.
If this task is done later in the year for Foundation-level students – and anytime for later years – students can be encouraged to record their responses numerically. For example, the solution found by moving two counters from the right-hand frame to the left, can be recorded as:
9 – 2 = 5 + 2
The possibilities of multiple answers gives students opportunities to compare the different types of equations, and to consider similarities and differences, for example:
9 = 5 + 4, 9 – 4 = 5, etc.
Teachers can encourage students to move beyond counting each counter each time, by reminding them that, ‘The top row contains 5 counters, because we have counted it before’. A possible learning intention for the task is: ‘We can make the collections equal and record our thinking with tens frames and number sentences.’
In discussing such a task, it is helpful for teachers to find a range of possible solutions and to discuss both the organisational and pedagogical issues associated with using such a task – especially in the early years. The explicit intention of describing this here is to emphasise that teacher commitment to such tasks is enhanced when school leaders are at the forefront of such discussions.
Another example of a classroom task suitable for students in Years 5-8 that focuses on equivalent fractions – depending on the level of sophistication expected – is outlined next.

The first step for teachers when considering a task such as this – whether in a teacher professional learning session or a team planning meeting – is to solve the task, preferably identifying all of the possibilities.
As an aside, readers are encouraged to find a systematic way to convince themselves that all possibilities have been found. There are four possible combinations, one of which is:

Then teachers can discuss the specific curriculum content descriptors potentially addressed through working on such a task, and ways in which the proficiencies are activated. In this case, students must first solve the problem, which includes:
- interpreting the problem statement
- finding a way to represent an answer
- checking that the answer actually solves the problem.
They can then explore ways of finding different possibilities. Such problem solving and reasoning helps to build understanding of the meaning of fractions, equivalent fractions and fraction addition. This, in turn, develops student fluency.
In the professional learning session or team-planning meeting, teachers can describe how this is similar to what they already do and how it is different, as well as discussing the opportunities for learning, the constraints they might anticipate and how the constraints might be overcome.
I emphasise that these tasks are presented as examples of the type of discussion that goes with choosing and discussing the potential of a task.
References
Sullivan, P., Bobis, J., Downton, A., Livy, S., Russo J., Stenning, P., & Giannopoulos, J. (2019). Exploring mathematical sequences of connected cumulative challenging tasks. Catholic Education Melbourne.
Leading Improvement in Mathematics Teaching and Learning, by Emeritus Professor Peter Sullivan, is published by ACER Press and available to order now via the link.



