In today’s article, Dave Tout, Justine Sakurai and Carly Sawatzki discuss numeracy and its relationship with mathematics, and the importance of real-world contexts. They’ll also share a problem-solving cycle to help students develop their skills and a classroom example of health numeracy, using trampolining as a focus for mathematical investigation.
Over the last couple of years, we have worked collaboratively to help shape and write Victorian senior secondary curricula that better supports the development of critical numeracy and maths skills in our school students. This is the first of two articles where we will share with you some of the research and theory that guided us, our thoughts about the purpose of education, and how these ideas influenced how we wrote those curriculum frameworks.
This first article will describe the background to our approach, and the second article will describe how we have attempted to espouse this in a curriculum document.
But first, what is, or are, our starting points? There are a few key elements behind our approach, including that:
- numeracy is the use and application of mathematical knowledge in context;
- numeracy is a social practice, which means there is always a clear purpose for learning that is connected to the real world;
- there is an implicit numeracy demand within most real-world problems; and,
- underpinning all this is a problem solving approach.
What is numeracy (and its relationships with mathematics)?
From our perspective, numeracy surrounds us in our everyday lives. Numeracy is about using mathematics to make sense of the world and applying mathematics in a context for a social purpose. For most young people and adults, numeracy gives meaning to mathematics, and mathematical knowledge and skills contribute to efficient and critical numeracy.
Students need a range of mathematical knowledge, skills, understandings and dispositions to solve problems in real contexts across personal, further learning, work, and community settings. To become numerate you need to know some mathematics. As Lynn Steen eloquently said:
...numeracy is not the same as mathematics, nor is it an alternative to mathematics. Today's students need both mathematics and numeracy. Whereas mathematics asks students to rise above context, quantitative literacy is anchored in real data that reflect engagement with life's diverse contexts and situations. (Steen, 2001, p.10)
Numeracy is not just about numbers and arithmetic. The mathematical knowledge and skills needed by all students includes number and quantity, measurement, shape, dimensions and directions, data and chance, and mathematical relationships and thinking. It also includes the ability to dip into your toolkit and choose and use the most appropriate analogue tools and digital technologies.
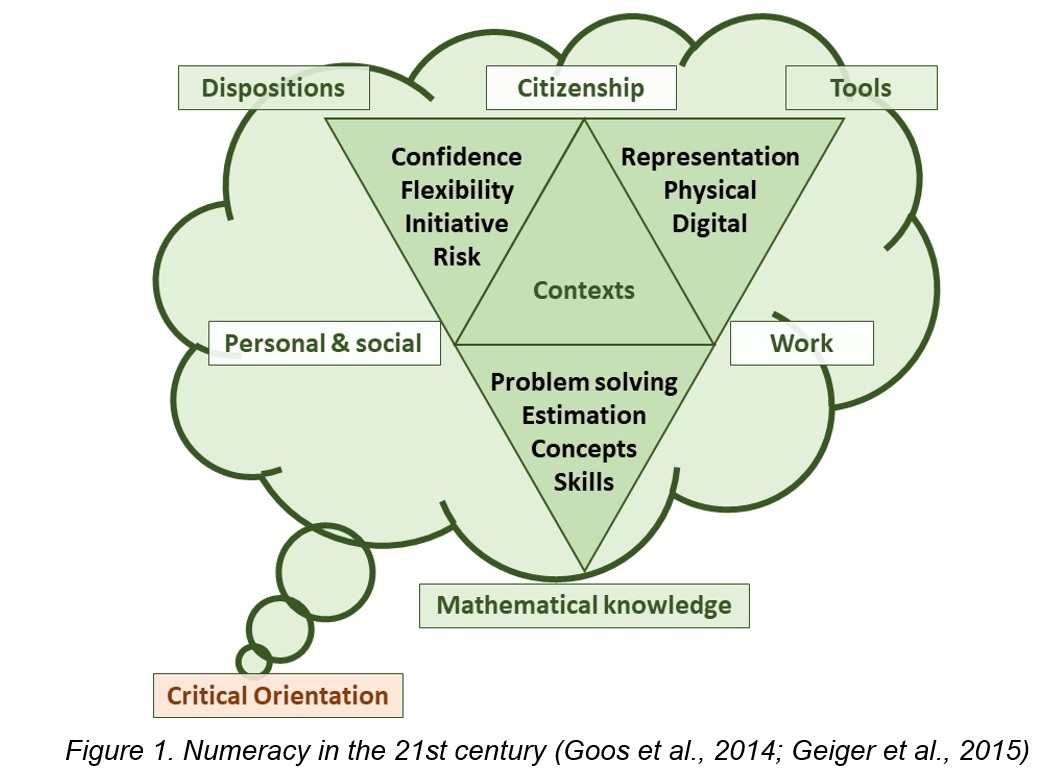
An Australian model of numeracy that we believe illustrates this perspective well is shown in Figure 1 below. This model incorporates four dimensions of contexts, mathematical knowledge, tools, and dispositions that are embedded in a critical orientation to using mathematics.
Why are real-world contexts so important?
Students often report that the mathematics they encounter at school feels disconnected from the real world. They express their frustration via the question, ‘When am I going to use this?’
Curriculum writers certainly intend that teachers bring their curriculum to life through contextualised lessons that connect with students’ real-world experiences. The complex challenges of modern life and work necessitate that schools deliver contextualised learning opportunities – students need higher levels of mathematics and numeracy than ever before and they need practise applying mathematics and numeracy to a range of familiar and unfamiliar authentic problems and issues (AAMT & AiGroup 2014; Binkley et al., 2012; FYA 2017; Gravemeijer et al., 2017).
As students become numerate, they develop the ability to make considered, mathematically-informed decisions, whether they be related to personal financial matters, planning travel arrangements, understanding and interpreting big data such as with the current COVID-19 epidemic, following instructions about a health or medical matter, or understanding the personal and social implications of problematic gambling.
Another of our key underpinning beliefs is that the exploration of real-world issues and problems is more valuable, satisfying and useful for students than the too frequent, often meaningless and repetitive practise of standard mathematical facts, procedures and processes. If students have little experience grappling with the messiness of real-world situations and problems, and if they can only apply mathematical procedures when problems are packaged in very familiar, structured ways (like in traditional maths classrooms and textbooks), then how can we expect them to value, see, use and apply maths in the world outside the classroom?
The AAMT and AiGroup research project referenced above documented this, with one of the teachers involved commenting on this disconnect:
This is one of the most interesting aspects/concepts of this project. The relationship between workplace mathematical skills and school mathematics could be described as ‘distant’ at best. Teacher observation (AAMT & AiGroup, 2014)
Being illiterate is considered an appalling state in modern Australia, yet evidence of significant numbers of students, especially young women, exiting the education system innumerate does not receive the same attention (ABS, 2013; OECD, 2017).
We believe therefore that we, as maths educators, need to support our students to be able to engage with and problem solve when maths is embedded in real-world situations and contexts, and this includes within our maths classrooms, as well as across the curriculum.
An underpinning problem-solving cycle
We believe that students need to develop the skills to problem solve, to investigate and solve a problem where the mathematics is embedded within a real-world context. The contexts should be the starting point, and students need well-planned and guided experiences with a structured problem-solving cycle, so that they know how to move from the real-world context to the mathematical world and apply their mathematical knowledge to find answers and solutions to the problem at hand.
An important aspect of numeracy is the ability to critically reflect on, evaluate and review your outcomes, and finally to be able to communicate and report on what you did and found.
In our curriculum endeavours, our suggested problem-solving cycle is modelled and adapted from the one used in the OECD's Programme for International Student Assessment (PISA) mathematical literacy assessment framework (OECD, 2019). This is consistent with the Figure 1 model. Our model has four distinct components, as represented in Figure 2 below.
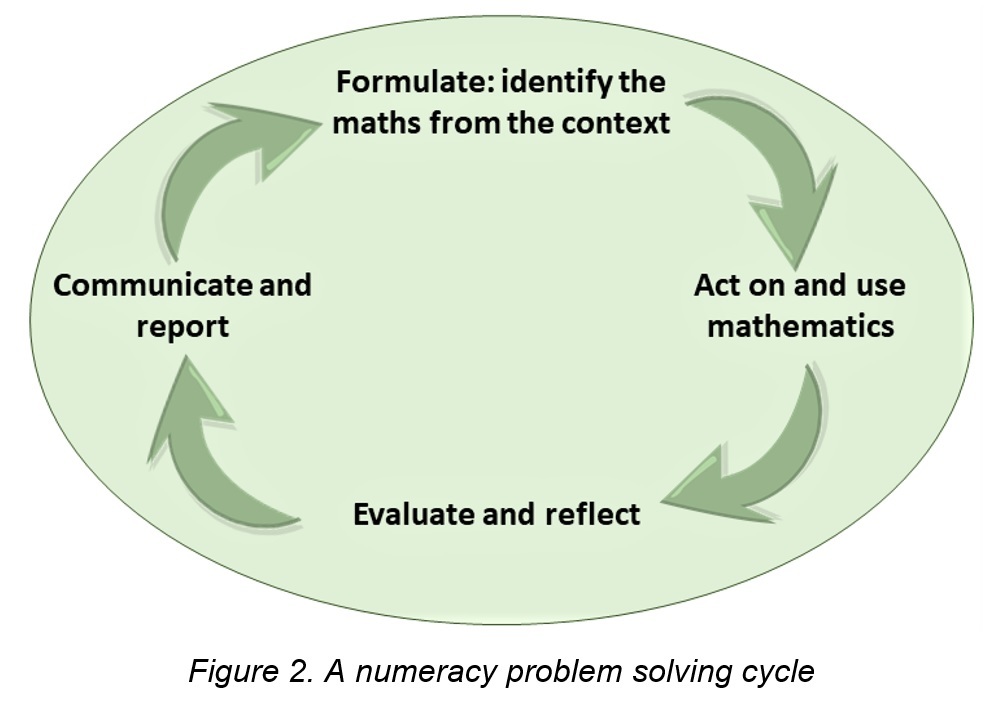
The four stages in the problem-solving cycle are:
- Formulate: where you need to identify, select, and interpret the mathematical information embedded in a real-world context and decide and plan what mathematics you need to use and what questions you might ask.
- Act on and use mathematics: in this stage you need to do the maths – perform the mathematical actions and processes so you can complete the task; this includes the use of a range of tools and technologies.
- Evaluate and reflect: here you are expected to check and reflect on both the mathematical processes you used and the reasonableness of your results and outcomes, especially in relation to the real-world context.
- Communicate and report: finally, there’s no point to the activity and investigations if you don’t document and report on your outcomes and any results. Here you need to use a combination of informal and formal mathematical representations.
Below is an example of an investigation taken from the context of health and fitness that illustrates the directions that teaching and learning can take when a numeracy problem-solving cycle is used in practice.
A classroom example – health numeracy
Health and safety related contexts provide interesting and useful opportunities to develop numeracy. Mathematical data and evidence can inform an understanding of risks, costs and benefits associated with such things as:
- Health and exercise
- Vaccination
- Prescription medications
- Alcohol and other drugs of addiction
- Medicare and health insurance
When an individual is informed, they are able to make better personal choices. This is not only good for the individual, their family and community, but can limit costs to the economy.
An example of a health and exercise context that might interest young people is trampolining. The backyard trampoline is a great tool in promoting health and fitness, and commercial trampolining centres are popular amongst young people.
The mock media report below includes statistical and numerical representations and language that underpin risk assessment and behaviour choices, and provides a context from which to initially introduce and study the problem. The ability to engage critically with and determine the trustworthiness of health reports presented by politicians, medical experts, journalists and social media influencers is essential.
Students might discuss:
- What is the probability (overall risk) of a spinal or head injury from trampolining?
- Do the benefits of trampolining outweigh the risks?
- What can be done to prevent accidents and injuries?
- What advice should be given to parents and children?
Once they identify the issues, they can mathematise the questions by unpacking the key concepts of probability and statistics using knowledge of fractions and percentages.
Student thinking may be extended by comparing safety figures between commercial centres, or health data from 20 years ago to today. Once students have considered the mathematics, reflecting on their findings should help them situate the problem and decide if the mathematics makes sense in the context.

A lesson may consider both aspects of the trampoline debate; cause of injuries, and building health.
A lesson sequence on trampoline health for younger students might consider asking students to keep a journal over a week or a month – how many times did they jump on their own or a friend’s trampoline? Students could consider how long each jumping session lasted for. They could break it down into ‘guesstimates’ of how much time was doing tricks, and how much time was straight jumps. They could conduct a survey and ask other students too. Their data could be displayed as a visual proportion on a line to aid in student development of estimation and proportional reasoning.

For an investigation, ask your students to estimate how many trampoline jumps would equal a two kilometre run? How would they work this out? Trampolining provides a real-life context that is relevant and applicable to students’ daily lives, through which they can learn using the problem-solving cycle.
There are many paths that may be taken as you and your students mathematise this problem. They may want to approach this problem using distance as a perspective by converting jumps into lengths? Another method may be for them to time how long it takes to run as opposed to jump? There are no limits to the approaches that may be employed in applying a mathematical lens to the problem. Be as creative and as physically active as you like when carrying out your mathematical investigations.
Once you have completed the mathematical tasking, the results must be looked at and interpreted within the context of the trampolining context. Ask your students to evaluate and reflect on their thinking: Has the question been answered and do the answers make sense in relation to the question? Finish by asking them to write up the results – get them to make a poster or a video.
Whatever angle you choose to take when designing problem-based tasks for your students, remember to keep it real, relatable, and relevant!
References
Ashby, K., Pointer, S., Eager, D., & Day, L. (2015). Australian trampoline injury patterns and trends. Australian and New Zealand journal of public health, 39(5), 491-494. https://doi.org/10.1111/1753-6...
Australian Association of Mathematics Teachers (AAMT) & Australian Industry Group (AiGroup). (2014). Tackling the School–Industry Mathematics Divide. Commonwealth of Australia. https://www.chiefscientist.gov... (PDF, 355KB)
Australian Bureau of Statistics. (2013). Programme for the International Assessment of Adult Competencies (Catalogue No. 4228.0). https://www.abs.gov.au/
Binkley, M., Erstad, O., Herman, J., Raizen, S., Ripley, M., Miller-Ricci, M., & Rumble, M. (2012). Defining twenty-first century skills. In P. Griffin, B. McGaw, & E. Care (Eds.), Assessment and Teaching of 21st Century Skills (pp. 17-66). Springer.
Carbonell, R. (2018, September 15). Double bounced: Why jumpy insurers are hopping out of the trampoline business. ABC News. https://www.abc.net.au/news/2018-09-15/trampoline-boom-loses-its-bounce-with-insurers/10249630
Foundation for Young Australians. (2017). The New Basics: Big data reveals the skills young people need for the New Work Order. FYA. https://www.fya.org.au/wp-content/uploads/2016/04/The-New-Basics_Update_Web.pdf (PDF, 1.5MB)
Geiger, V., Goos, M., & Forgasz, H. (2015). A rich interpretation of numeracy for the 21st century: A survey of the state of the field. ZDM Mathematics Education, 47(4), 531-548. https://doi.org/10.1007/s11858-015-0708-1
Goos, M., Geiger, V., & Dole, S. (2014). Transforming professional practice in numeracy teaching. In Y. Li, E. Silver, & S. Li (Eds.), Transforming Mathematics Instruction (pp. 81-102). Springer. https://doi.org/10.1007/978-3-319-04993-9_6
Gravemeijer, K., Stephan, M., Julie, C., Lin, F. L., & Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? International Journal of Science and Mathematics Education, 15(1), 105-123. https://doi.org/10.1007/s10763-017-9814-6
Michie, F. (2015, September 11). Rise in serious trampoline injuries in children worries trauma specialists, prompts new research. ABC News. https://www.abc.net.au/news/2015-09-11/rise-in-trampoline-injuries-worries-trauma-specialists/6766536
OECD. (2017). Building Skills for All in Australia: Policy Insights from the Survey of Adult Skills. OECD Skills Studies, OECD Publishing. https://doi.org/10.1787/9789264281110-en.
OECD. (2019). PISA 2018 Assessment and Analytical Framework. PISA, OECD Publishing. https://doi.org/10.1787/b25efab8-en.
Sharwood, L. N., Adams, S., Blaszkow, T., & Eager, D. (2018). Increasing injuries as trampoline parks expand within Australia: a call for mandatory standards. Australian and New Zealand Journal of Public Health, 42(2), 153-156. https://doi.org/10.1111/1753-6405.12783
Steen, L. (2001). Mathematics and Numeracy: Two Literacies, One Language. The Mathematics Educator, (6)1, 10-16.
With a colleague, consider a problem-based task you’ve used in one of your own lessons. Was this problem real, relatable and relevant to your students, their context and experiences? Now, work together to design a new task for an upcoming lesson or topic area that meets these requirements.