There has been considerable research about students' difficulties with fraction tasks and the possible misconceptions their solutions may reveal if allowed to articulate their thinking either orally or in writing.
Many students get the correct answers to mathematics tasks even though their thinking is incorrect. Students may ‘self-correct' if given the opportunity to explain their response to a mathematical task.
In this article, we'll use students' responses to four fraction tasks to focus on possible ‘faulty' thinking (or misconceptions) that allow them to get the correct answer, even though their thinking is incorrect. The four fraction tasks have been used with students from Years 5 to 9.
a. Choosing the larger of two fractions
b. Ordering four fractions
c. Naming the four interim marks on a number line marked 0 – 100
d. Showing where 75 fits on a number line when the section 0 – 25 is marked
a. Choosing the larger of two fractions
As part of a short Fraction Probing Interview (Pearn & Stephens, 2004) Year 8 students were asked to decide which fraction was larger from each of the following pairs of fractions:

If solving these types of tasks in class, students could use concrete materials such as fraction walls or fraction cakes or fold paper strips to compare each of these pairs of fractions. However, during the interview Year 8 students used written and mental calculations.
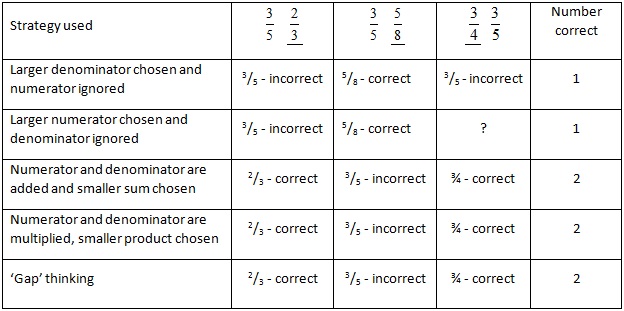
Many successful students relied on forming equivalent fractions, as would be expected at Year 8. For example, when comparing 3/5 and 2/3 many students found the Lowest Common Multiple (15) and converted 3/15 to 9/15 and 2/3 to 10/15 – thus allowing them to correctly state that two-thirds (10/15) was larger than three-fifths (9/15). However, students used other methods to calculate which of the two fractions was the larger. Many students had developed their own ways of comparing fractions that included thinking such as:
- The larger the denominator the larger the fraction. In this case students completely disregard the numerator.
- The larger the numerator the larger the fraction. The denominator is usually ignored or in some cases is ordered according to size if there are multiple numerators of the same size.
- The numerator and denominator are either added or multiplied and the smaller result chosen “because fractions are different to whole numbers”.
- The difference or ‘gap' between the numerator and denominator is found and the smaller the gap then students believe the larger the fraction (‘gap' thinking). Many students consider 3/4 to be a large fraction because “you only need one more to make the whole”.
In the table below, we will consider whether the thinking of the students leads to a correct or incorrect choice. The larger fraction of each pair is underlined.
Table 1: Choice of larger fraction according to strategy used
b. Ordering fractions
In this task some students were able to order the fractions from largest to smallest with other students successfully ordering the fractions from smallest to largest. Students who successfully ordered the fractions used equivalent fractions by choosing 20 as the Lowest Common Denominator so that 1/2 was rewritten as 10/20, 1/4 as 5/20, 3/5 as 12/20 and 1/10 as 2/20.

Students' faulty thinking when ordering fractions replicated the thinking used for the Choosing the Larger Fraction task.
Table 2: Ordering fractions according to strategy used
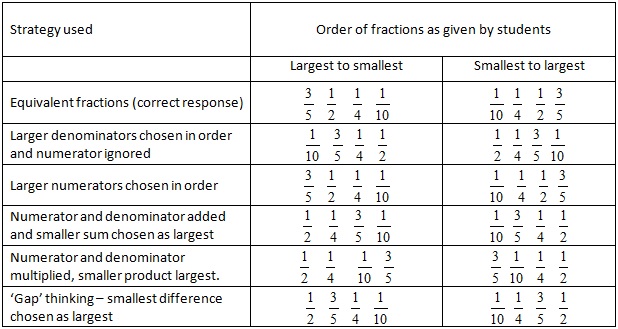
In Table 2, you can see that students using the ‘larger numerator' to order the fractions may well have chosen the correct order depending on how they ordered the unit fractions of one-half, one-quarter and one-tenth. Different choices of fractions to be ordered may allow students to give correct responses even though their thinking is incorrect.
c. Marking the divisions on a number line
This task requires students to determine which whole numbers should be placed on the four marks between 0 and 100. The line has been divided into five equal parts and the task becomes much simpler if students realise they can divide 100 into five equal parts. Thus, they are completing a fraction task without the complication of using fractional language.

Many students try counting by tens before trying counting by 20. When asked to explain how they decided they are correct these students refer to ‘counting '. If the number on the end of this number line was changed to one or two this counting strategy would be less likely to be used as students are not used to counting by fifths. However, students who focus on the number of parts and ‘divide 100 by 5' will easily and successfully complete the relevant division if the numbers on the number line are changed.
d. Using the divisions on a number line
This task requires students to use the distance from 0 – 25 initially to mark where the number 50 would be, and then use the distance a second time to place 75. However, many students assumed that the end of the line was 100 so halved the whole line to find 50 and then halved the last half of the line to find three-quarters of the line, which they marked as 75.

In this task three-quarters of the line is fairly close to the correct response, so asking students to explain how they know their answer is correct is really the only way of determining their thinking. Dividing the number line into parts is a much easier task than having to start with a known part and replicating it.
In the four tasks given above I have shown that students can get the correct response to fraction tasks even though their thinking is faulty.
Students must develop an understanding of the size of fractions using concrete materials such as paper folding and fraction walls. Using fraction walls students can find equivalent fractions and fractions that are smaller, or larger, than other fractions.
Number lines are also important in developing the notion of the density of the number line. Starting with number lines marked with whole numbers allows students to find fractional parts of a number line without the fractional language, however there must be a transition to using fractions to mark number lines and to determine the length of the number line.
References
Pearn, C. & Stephens, M. (2004). Why you have to probe to discover what Year 8 students really think about fractions. In Putt, I., Faragher, R., & McLean, M. (Eds.), Mathematics Education for the third millennium: Towards 2010. Proceedings for the 27th annual conference of the Mathematics Education Research Group of Australasia (MERGA-27). Townsville, Queensland: MERGA. Retrieved from https://www.merga.net.au/documents/RP512004.pdf
How often do you allow students the chance to explain their response to a maths task?
Are you aware of the possible misconceptions students may have as they solve maths tasks?
As a teacher, what strategies do you use to draw out ‘faulty’ thinking or misconceptions?
Do you check the understanding of students who get the right answer, as well as those who don’t?



